Leetcode-maxSubArray

最大子序和

问题描述

给定一个整数数组 nums ，找到一个具有最大和的连续子数组（子数组最少包含一个元素），返回其最大和。

来源：力扣（LeetCode）

示例

示例 1：
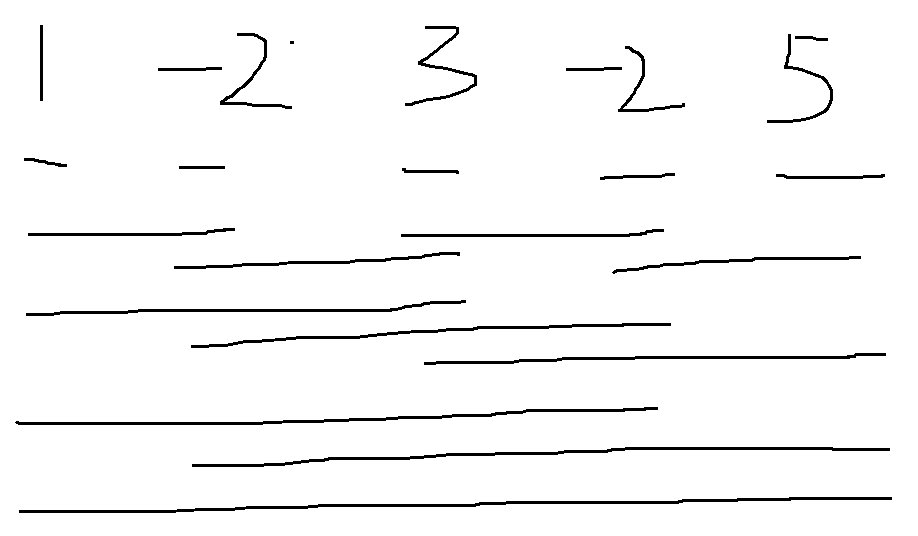
输入：nums = [-2,1,-3,4,-1,2,1,-5,4]
输出：6
解释：连续子数组 [4,-1,2,1] 的和最大，为 6 。

示例 2：
输入：nums = [1]
输出：1

示例 3：
输入：nums = [0]
输出：0

示例 4：
输入：nums = [-1]
输出：-1

示例 5：
输入：nums = [-100000]
输出：-100000

思路

• 暴力法1

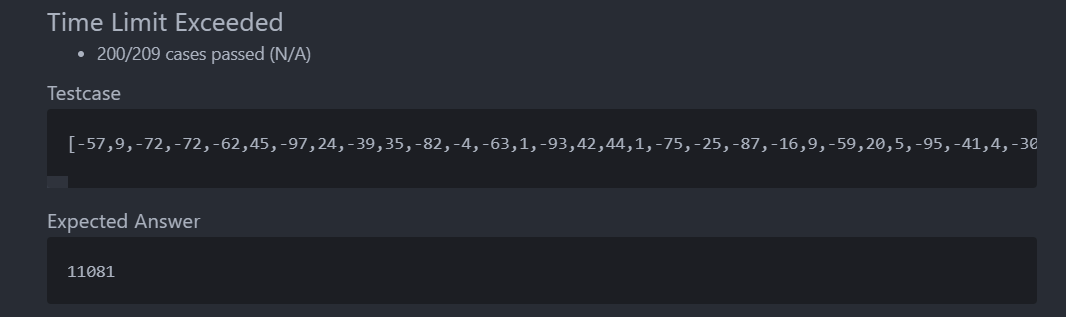
结果果然超时T_T(时间复杂度：O(n³))

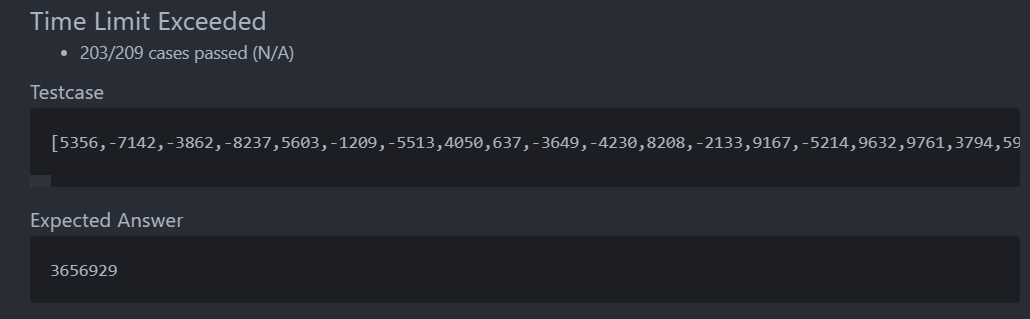
• 暴力法2

时间复杂度：O(n²)

• 贪心法

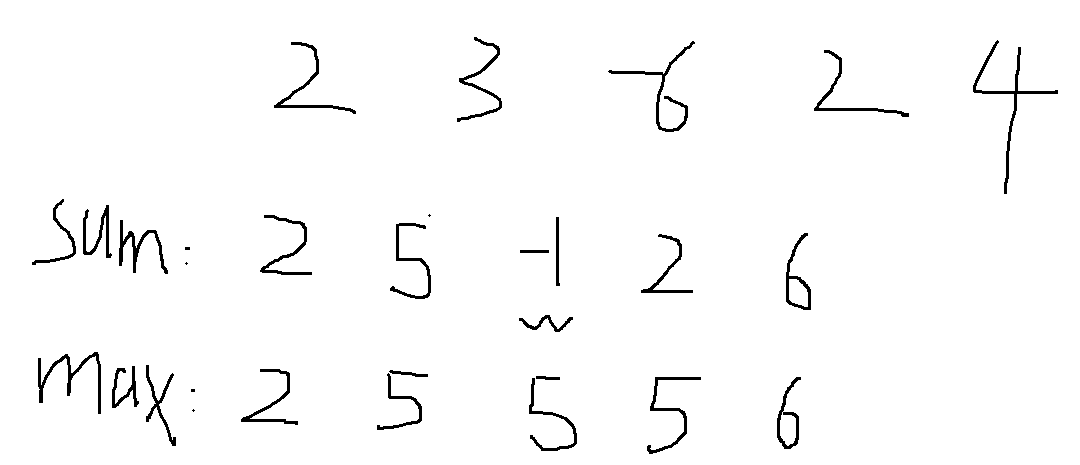
时间复杂度：O(n)

代码

暴力法1

class Solution {
public:
    int maxSubArray(vector<int>& nums) {
        int sum = nums[0];
        for (int i = 1; i <= nums.size(); i++) //控制子数组长度
        {
            for (int j = 0; j <= nums.size() - i; j++) //子数组起始元素
            {
                int total = 0;
                for (int k = 0; k < i; k++) //计算子数组和
                {
                    total += nums[k + j];
                }
                if (total > sum) //保存当前最大子数组和
                {
                    sum = total;
                }            
            } 
        }
        return sum;
    }
};

暴力法2

class Solution {
public:
    int maxSubArray(vector<int>& nums) {
        int sum = nums[0];
        for (int i = 0; i < nums.size(); i++) 
        {
            int total = 0;
            for (int j = i; j < nums.size(); j++)
            {
                total += nums[j];
                if (total > sum)
                {
                    sum = total;
                }          
            }     
        }
        return sum;
    }
};

贪心法

class Solution {
public:
    int maxSubArray(vector<int>& nums) {
        int sum = 0;
        int result = nums[0];
        for (int i = 0; i < nums.size(); i++) 
        {
            sum += nums[i];
            result = max(result, sum);
            if (sum < 0)
            {
                sum = 0;
            }     
        }
        return result;
    }
};

结果